Python Set Operation

 

Set Operations

Set objects also support mathematical operations like union, intersection, difference, and symmetric difference.

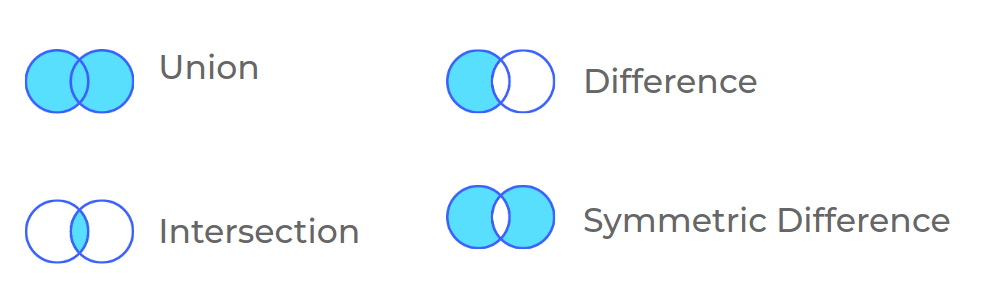
Union

Union of two sets is a set containing all elements of both sets.

set_a | set_b

or

set_a.union(sequence)

union()

converts sequence to a set, and performs the union.

Code

1

2

3

4

set_a = {4, 2, 8}

set_b = {1, 2}

union = set_a | set_b

print(union)

PYTHON

Output

{1, 2, 4, 8}

Code

1

2

3

4

set_a = {4, 2, 8}

list_a = [1, 2]

union = set_a.union(list_a)

print(union)

PYTHON

Output

{1, 2, 4, 8}

Intersection

Intersection of two sets is a set containing common elements of both sets.

set_a & set_b

or

set_a.intersection(sequence)

intersection()

converts sequence to a set, and perform the intersection.

Code

1

2

3

4

set_a = {4, 2, 8}

set_b = {1, 2}

intersection = set_a & set_b

print(intersection)

PYTHON

Output

{2}

Code

1

2

3

4

set_a = {4, 2, 8}

list_a = [1, 2]

intersection = set_a.intersection(list_a)

print(intersection)

PYTHON

Output

{2}

Difference

Difference of two sets is a set containing all the elements in the first set but not second.

set_a - set_b

or

set_a.difference(sequence)

difference()

converts sequence to a set.

Code

1

2

3

4

set_a = {4, 2, 8}

set_b = {1, 2}

diff = set_a - set_b

print(diff)

PYTHON

Output

{8, 4}

Code

1

2

3

4

set_a = {4, 2, 8}

tuple_a = (1, 2)

diff = set_a.difference(tuple_a)

print(diff)

PYTHON

Output

{8, 4}

Symmetric Difference

Symmetric difference of two sets is a set containing all elements which are not common to both sets.

set_a ^ set_b

or

set_a.symmetric_difference(sequence)

symmetric_difference()

converts sequence to a set.

Code

1

2

3

4

set_a = {4, 2, 8}

set_b = {1, 2}

symmetric_diff = set_a ^ set_b

print(symmetric_diff)

PYTHON

Output

{8, 1, 4}

Code

1

2

3

4

set_a = {4, 2, 8}

set_b = {1, 2}

diff = set_a.symmetric_difference(set_b)

print(diff)

PYTHON

Output

{8, 1, 4}

Set Comparisons

Set comparisons are used to validate whether one set fully exists within another

• issubset()
• issuperset()
• isdisjoint()

Subset

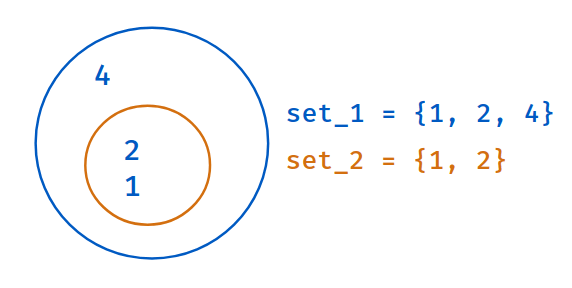
set2.issubset(set1)

Returns

True

if all elements of second set are in first set. Else,

False

Example - 1

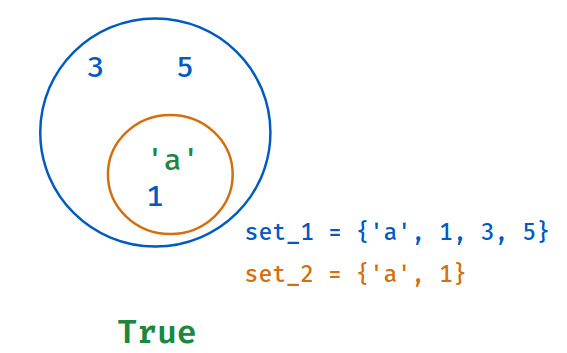
Code

1

2

3

4

set_1 = {'a', 1, 3, 5}

set_2 = {'a', 1}

is_subset = set_2.issubset(set_1)

print(is_subset)

PYTHON

Output

True

Example - 2

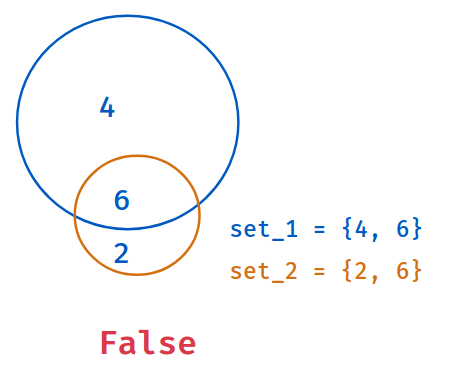
Code

1

2

3

4

set_1 = {4, 6}

set_2 = {2, 6}

is_subset = set_2.issubset(set_1)

print(is_subset)

PYTHON

Output

False

SuperSet

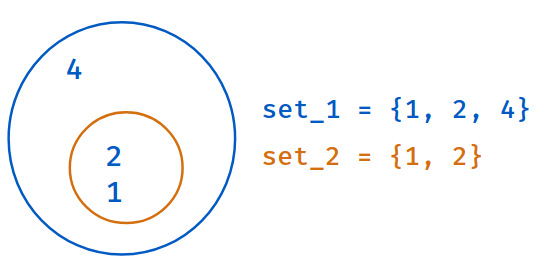
set1.issuperset(set2)

Returns

True

if all elements of second set are in first set. Else,

False

Example - 1

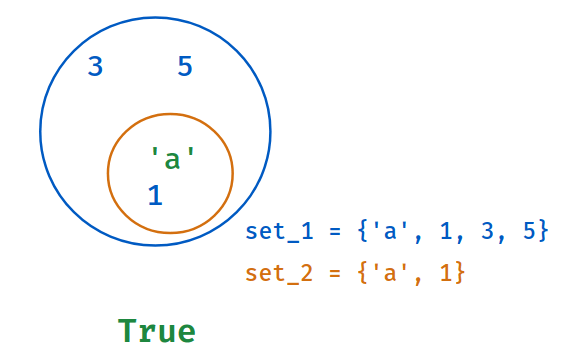
Code

1

2

3

4

set_1 = {'a', 1, 3, 5}

set_2 = {'a', 1}

is_superset = set_1.issuperset(set_2)

print(is_superset)

PYTHON

Output

True

Example - 2

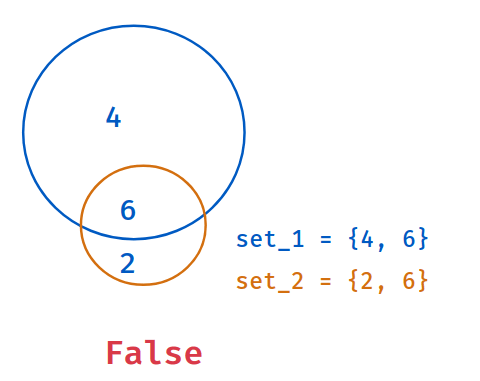
Code

1

2

3

4

set_1 = {4, 6}

set_2 = {2, 6}

is_superset = set_1.issuperset(set_2)

print(is_superset)

PYTHON

Output

False

Disjoint Sets

set1.isdisjoint(set2)

Returns

True

when they have no common elements. Else,

False

Code

1

2

3

4

set_a = {1, 2}

set_b = {3, 4}

is_disjoint = set_a.isdisjoint(set_b)

print(is_disjoint)

PYTHON

Output

True